こんにちは!
天気が良すぎるので2駅分歩いたミヨです。
妹にダイエットを教えて数日経ちますが、
「1日に何食にした方がいいの?」
と質問をされました。
あ〜。
そういえば、1日1食うんぬんを言ってる
お医者さんがいたなぁ。
って妹の一言で思い出しましたよ。
答えとしては
『自分がちょうどいい回数ならいいよ』
で終了です(⌒-⌒; )
さすがに
こんな答えで終わるのはイカンので、
ちゃんとお答えします…
食事の回数にこだわらなくていい
食べられるのであれば
1日に5食でもいいし、
平気なら1食でいいんですよ。
お腹が空いてるのに
ガマンして1食で済ませるとか、
お腹いっぱいなのに
5食も6食も食べるのが問題なだけで。
わたしは1食じゃ元気でないし、
5食にする食事量の配分や
時間がとれないので
2食または3食がちょうどいいですね。
無理して1食とか5食にはしなくていいです。
もし
1食や5食にしたいと思っているのなら、
それぞれのデメリットを
知っておいてください。
1日1食では栄養・カロリー不足
ツイッターで
「1日に食事は1回にしろ。
そうすれば痩せる」
ってあったんですよ。
うん。まあそうだよね。
食事減らせば痩せるよ。
ただし、おかしな痩せ方するけどね。
たまに1食だけで余裕で過ごせる
なんて人もいますが、
身体がエネルギーを使わないよう
エコに切り替わってるからだと思います。
1日に必要なカロリー・栄養を
たった1回の食事ですべて賄うのって
ほぼ無理です。
だって
朝・昼・夜の3回の食事を
1回ですべて食べきるんですよ?
現在のあなたの1日の食事を思い出してください。
その食事を1回で食べられますか?
無理ですよね?
たぶん
食べれたとしても
1,000kcalがやっとじゃないかと。
カロリーが足りなくなれば
甘いものを欲してしまうし、
栄養が足りなくなれば
体調にも関わってきます。
「食べたいけど、ガマン」
これじゃあストレスしかないので、
食事が楽しめません。
誰かと食事をする機会も少なくなるし、
美味しい体験ができるチャンスも
捨てることになります。
1日1食の健康法がありますけど、
こういうデメリットがあることも
ちゃんと理解してくださいね。
1日5食は食欲・時間管理が大変
食事の回数は
増やした方が太りにくくなる。
これは本当です。
ただし、
1日に必要な栄養やカロリーを
5回6回の食事に分ける。
という意味なので
1回あたりの食事量は少なくなります。
少量を数時間おきに食べるのって、
普通の生活してたら難しくない?
さっき食べたのに、
また食べないといけない。
そもそも時間取れないし。
食べ過ぎて気持ち悪くなってきた。
食事量の配分ってなかなか難易度が高いので、
なんの知識・準備もなしに始めるのは
危険かなぁと思います。
仕事・家事・育児に追われてたら、
食事をすることさえも忘れることだって
ありますし。
食事って、回数を増やすほど
食べる時間や、栄養配分、
食欲の管理が難しくなります。
これはプロでも難易度が高いので、
全員に勧めるような食事法ではないですね。
管理栄養士という資格を持ってますけど、
わたしはやれません。
細かく食事をする時間が取れないので(⌒-⌒; )
食事の回数はお好きにどうぞ
妹からの質問の答えとしては、
はじめに言った通り
『自分がちょうどいい回数で』
となります。
1回で平気なら、1日1食の生活でもいいし。
3回がちょうどいいなら、それでOKです。
食べ過ぎや
栄養・カロリー不足の原因になるので
食事の回数に変にこだわる必要はないです。
食事が楽しいものでなくなること。
ストレスの原因になってしまうことが
一番いやなので。
わたしだって1日に2食になる日もあります。
それはお腹が空かないから
というのが理由です。
それでも
栄養の質やバランスには注意してますけど。
無理して食べる、食べたいけどガマン
これをしてないので、
食事に関するストレスは少ないです。
やっぱり
食事は楽しくなきゃ続けられません(`・∀・´)



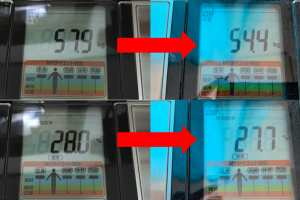








 →
→  …→
…→
コメントを残す